Method 1 – Using Direct Formula to Calculate Monthly Payment
This is the mathematical formula that calculates monthly payments:
M = (P*i)/(q*(1-(1+(i/q))^(-n*q)))
Here,
- M is monthly payments
- P is the Principal amount
- i is the Interest rate
- q is the number of times a year you will make the payments
- n is the number of years you get to pay off the whole loan and its interest
Consequently, we can use this formula in Excel to find the monthly payments. Check out the following steps.
Step 1:
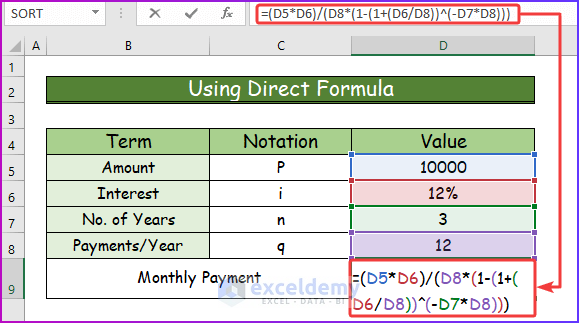
- Write the following formula in cell D9.
=(D5*D6)/(D8*(1-(1+(D6/D8))^(-D7*D8)))- Assume the cell values are the terms from the main formula.
Step 2:
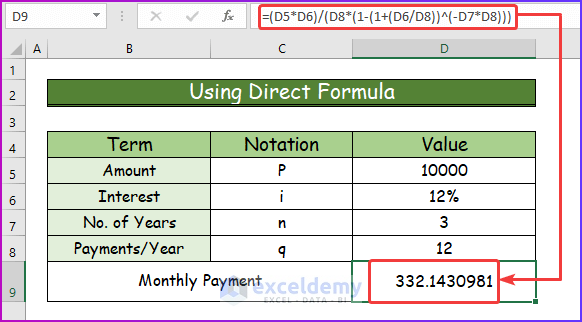
- Press Enter to see the monthly payment for repaying the loan.
- The user has to pay this amount for three years to repay the loan.
Method 2 – Applying PMT Function to Calculate Monthly Payment
Summary:
- The PMT function determines the payment to repay a loan where a fixed interest rate is provided.
- Available from Excel 2007.
Syntax:
The formula or syntax for the PMT function in Excel is,
PMT(rate, nper, pv, [fv], [type])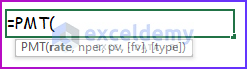
Arguments:
| Arguments | Required or Optional | Description |
|---|---|---|
| rate | Required | Interest rate per period. Say, you got a loan at a yearly interest rate of 12%.
|
| nper | Required | The total number of payment periods. Say you got the above loan for the next 5 years.
|
| pv | Required | The present value. Simply, it is the loan amount you receive. |
| fv | Optional | Future value. When you calculate the loan payment, in most cases, this value will be 0. At the end of your last payment, there will be no balance with the bank. If you don’t use this value, PMT will assume this value as 0. |
| type | Optional | The type takes two values:
|
Return:
The PMT function returns the payments to repay the loan as a value.
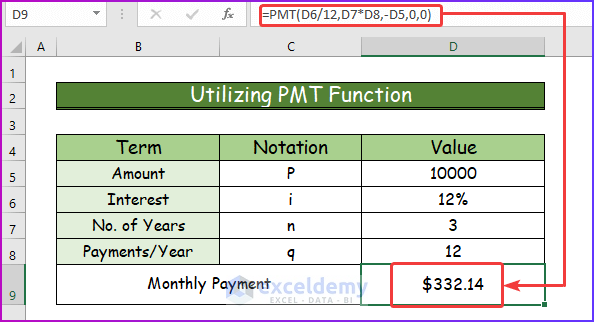
2.1 Utilizing PMT Function
After discussing the PMT function, I will demonstrate its application to calculate the monthly payment.
Step 1:
- Insert the following formula of the PMT function in cell D9.
=PMT(D6/12,D7*D8,-D5,0,0)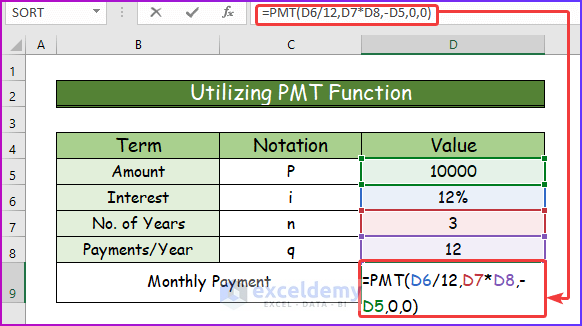
Step 2:
- After pressing Enter, considering all the given arguments, the function will show the monthly payment.
- The yearly interest rate is 12%. So, the per-month interest rate is 12%/12 = 1%. The PMT function’s rate argument is 1%.
- The principal amount, the amount you took from the bank, is $10,000. So, the PMT function’s pv is 10,000.
- The number of years you’ll have to pay off the principal and interest is 3. This is a monthly payment, so the total number of periods you will get is 3 years x 12 = 36 months. Nper is 60.
- In cell C10, the PMT function will show a value of $332.14. The value is positive as I have used a negative sign (-ve) before the loan amount. The PMT function gives negative values.
2.2 PMT Function with Compounded Period
Let’s show you something different than what we have done so far.
Check out this scenario:
- Loan amount $10,000
- Interest rate 12%
- Monthly Payment
- But the interest rate is compounded semi-annually
- Payment periods 3 years = 36 months
A little bit critical case.
Think along with me:
- The interest rate will be compounded semi-annually (every 6 months), right? So, divide 12% by 2 which returns 6%.
- Payments are monthly. So, over the 6 months of payments, you will pay an overall 6% interest rate. If you think mathematically, it will be like (1+x)^6 = 1.06 where is x is your monthly interest over the 6 months of payments. It is easy now to calculate the value of x from this equation => x = 06^(1/6) – 1 = 0.00975879. The value of x is 0.00975879.
See the following steps to apply this concept in Excel.
Step 1:
- Insert the following formula in cell C7 to calculate the monthly payment.
=PMT((C4/2+1)^(1/6)-1,C6,-C5)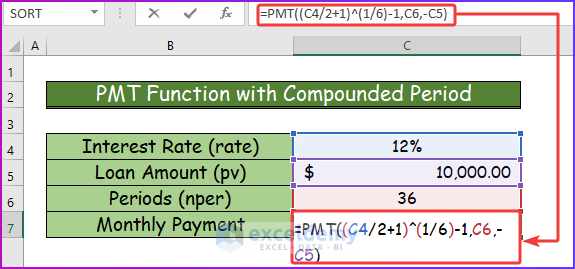
Step 2:
- Hit Enter to get the desired result.
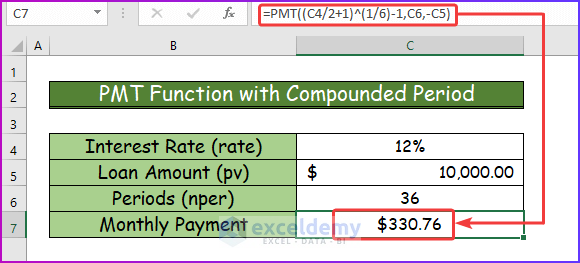
Formula Breakdown
(C2/2+1)^(1/6)-1:
- The value of C2 is 12%, so C2/2 = 12%/2 = 6%
- C2/2+1 = 6% + 1 = 06
- This part of the formula comes into this form: 06^(1/6) – 1 which results in the value 00975879.
Calculating Monthly Interest Rate in Excel
Aside from calculating the monthly payment, you can also calculate the monthly interest rate in Excel. You will have to use the RATE function of Excel which returns the interest rate per period of a loan. See the below-given steps to calculate the monthly interest rate on loans in Excel.
Step 1:
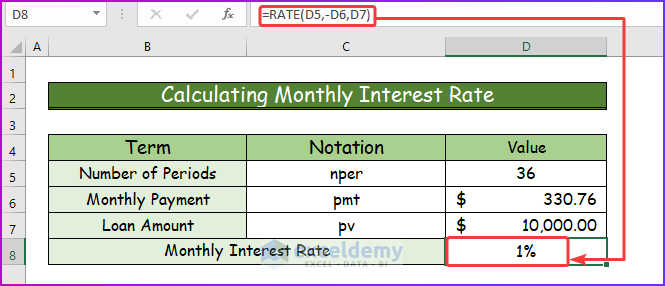
- To calculate the interest rate, take the following data set with all the necessary arguments.
- In cell D8, use the following formula of the RATE function.
=RATE(D5,-D6,D7)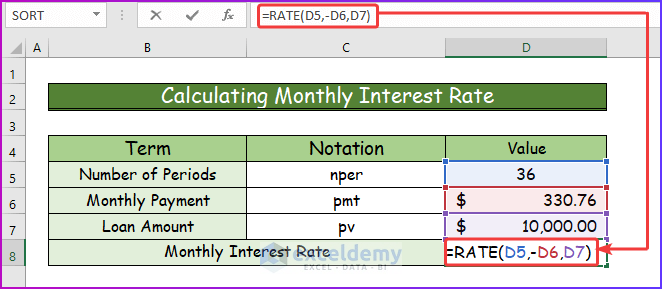
Step 2:
- After pressing Enter, the monthly interest rate is 1%.
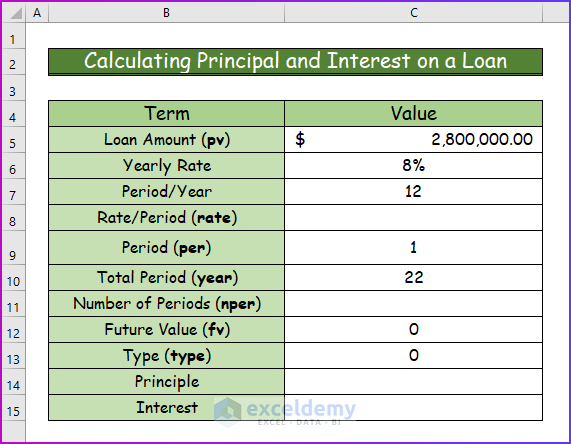
Calculating Principal and Interest on a Loan in Excel
Step 1:
- Take the following data set with all the necessary arguments.
Step 2:
- To calculate the rate, use the following formula in cell C8.
=C6/C7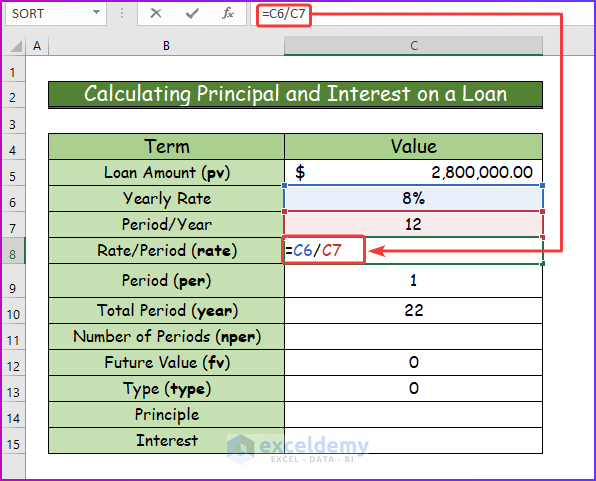
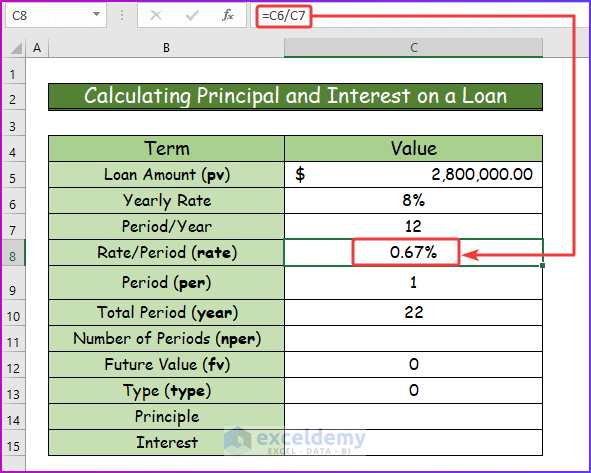
Step 3:
- Press Enter to get the value for rate in cell C8.
Step 4:
- To calculate nper, input the following formula in cell C11.
=C10*C7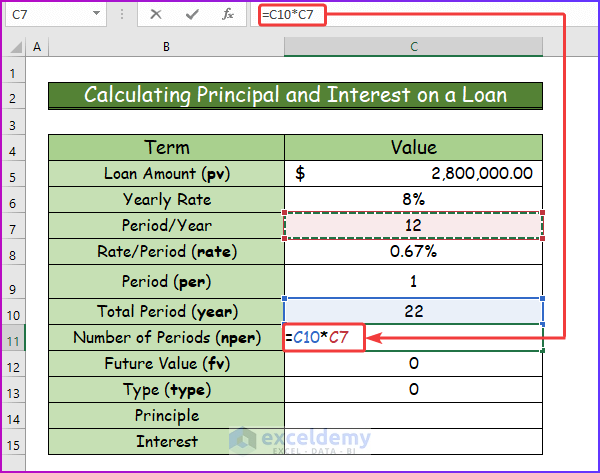
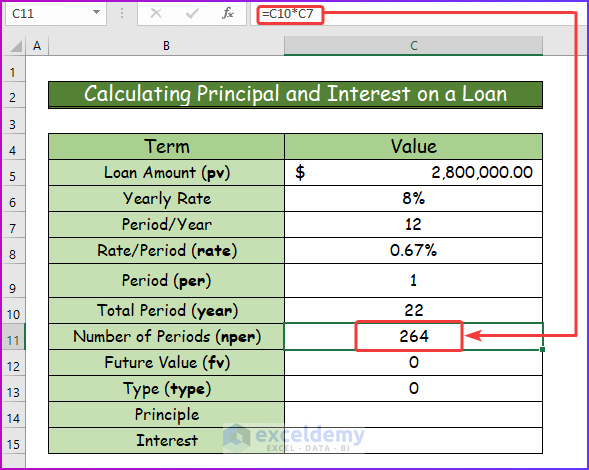
Step 5:
- After pressing Enter, you will get the result in a numeric value for nper.
Step 6:
- Calculate the principal and interest after finding out all those previous values.
- Calculate the principal, type the following formula of the PPMT function in cell C4.
=PPMT(C8,C9,C11,-C5,C12,C13)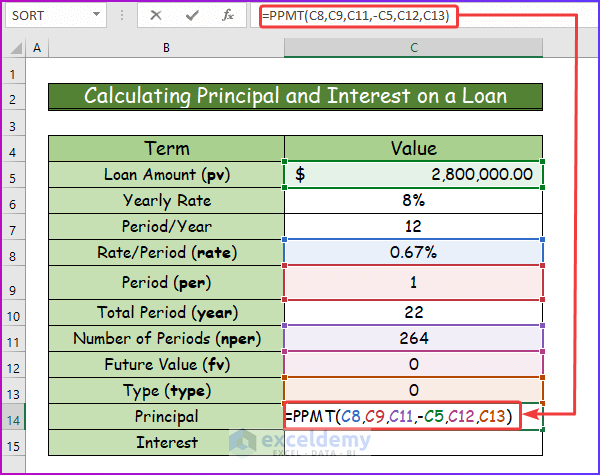
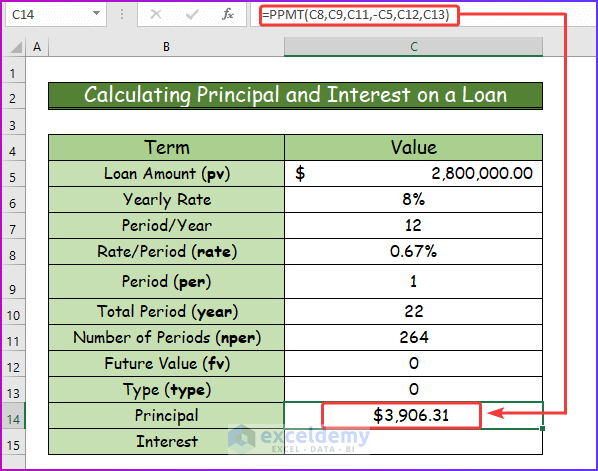
Step 7:
- Press the Enter button to get the desired result.
Step 8:
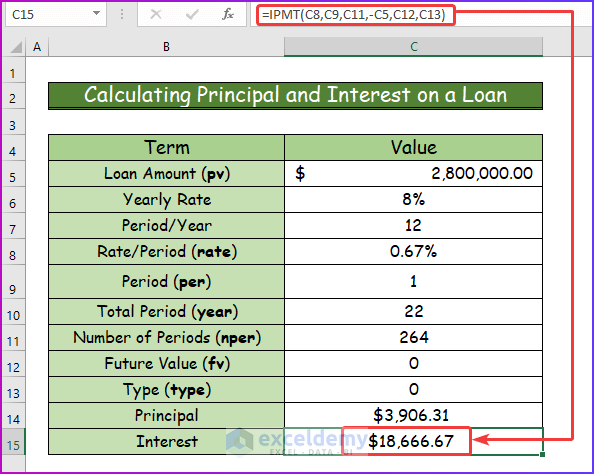
- Calculate interest and insert the following formula of the IPMT function in cell C15.
=IPMT(C8,C9,C11,-C5,C12,C13)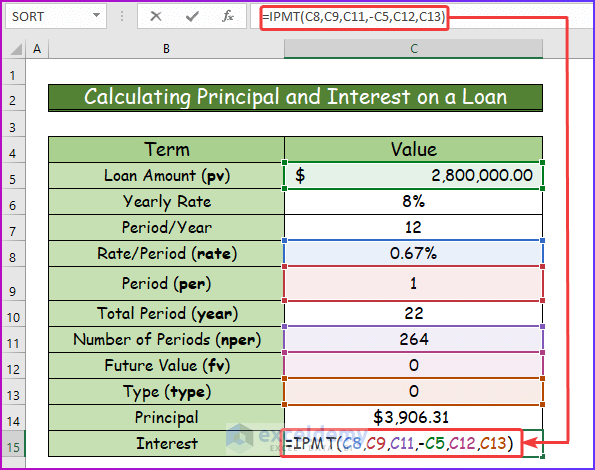
Step 9:
- Get the desired result by pressing Enter, after inserting the above formula.
Download Practice Workbook
You can download the free Excel workbook here and practice on your own.
Related Articles
- How to Calculate Car Payment in Excel
- How to Calculate Monthly Mortgage Payment in Excel
- How to Calculate Down Payment in Excel Using VLOOKUP
- How to Calculate Coupon Payment in Excel
- How to Calculate a Lease Payment in Excel
- How to Calculate Balloon Payment in Excel
<< Go Back to Calculate Payment in Excel | Excel for Finance | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!


i was thinking if you can make a dashboard for a few rental property just the thought
Thanks for the suggestion 🙂 I will keep it on my list.
Do you have daily rest interest calculation? I don’t see in your worksheet.
Thanknyou
In case it wasn’t posted.
What about daily interest calculation?
Home loan has daily compounding interest calculation.
Thank you
Would you mind if you show how to calculate interest compounded monthly on an outstanding late invoices.
for example, several invoices haven’t been paid after the due date, for a number of customers, and we’re going to charge 7% (Yearly), compounded monthly. how to keep track for the ongoing balance on a table for all customers ?
Hope you can find way to make it on one table..
Thank you …
Hello Wasim,
I am keeping this on my to-do list. Will try to give you a solution of your problem.
Thanks.