What Is the BMI?
BMI (Body Mass Index) is a standard index first proposed by Adolphe Quetelet in the 1830s. It gives an insight into a person’s physical fitness status. The formula involves Height and Weight. The general expression of BMI is:
BMI=Weight/Height2
What Is Z Score?
The basic formula for the calculation of the Z Score is given below:
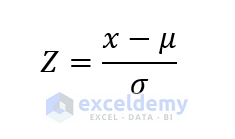
x = The raw data.
µ = Mean/Average of the dataset.
σ = The standard deviation of the given dataset.
Z = Final score of each data.
The Z Score shows the distance of data from the Mean in the Standard Deviation unit. If it’s 0, the value is in the mean value.
If the Z Score is 1, the value is 1 Standard Deviation above the Mean value. If it’s -1, the value is a Standard Deviation below the Mean value.
How to Calculate BMI Z Score in Excel – 4 Steps
In the following dataset, height and weight of patients are listed.
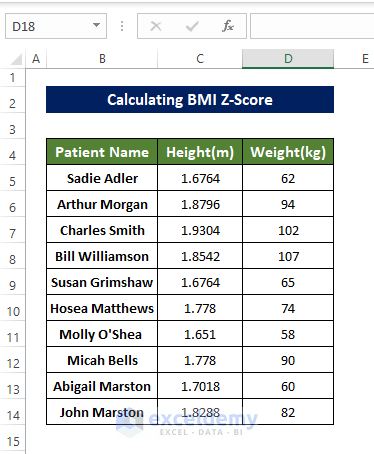
Step 1 – Prepare the Dataset
- Convert the data to Metric Units: Weight in KG and Height in Meters.
Step 2 – Calculate the BMI
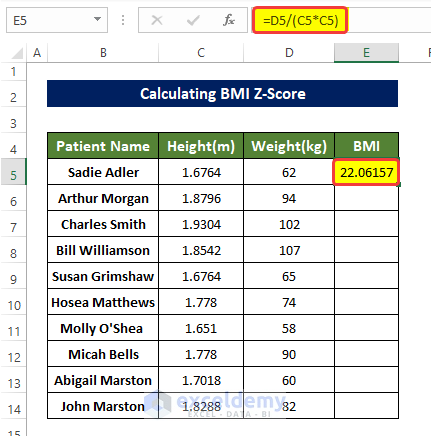
- Select E5 and enter the following formula:
=D5/(C5*C5)The BMI is calculated.
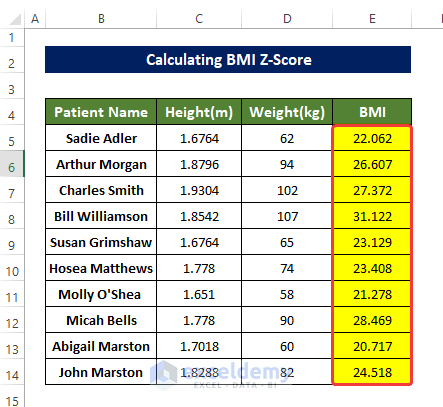
- Drag down the Fill Handle to see the result in the rest of the cells.
Step 3 – Calculate the Standard Deviation and Mean of the Dataset
Steps
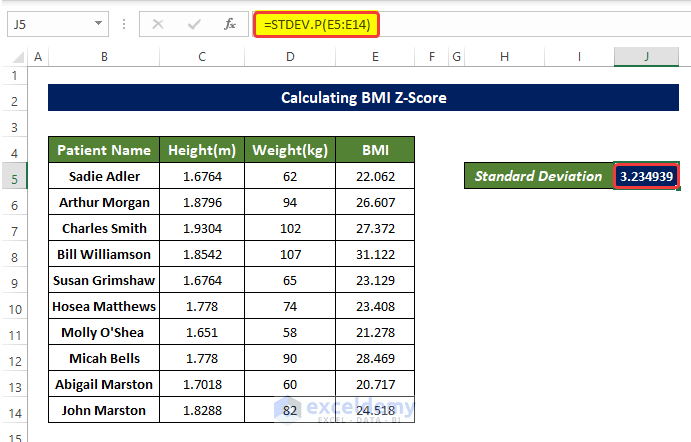
- Select J5 and enter the following formula:
=STDEV.P(E5:E14)- It will calculate the Standard Deviation in E5:E14.
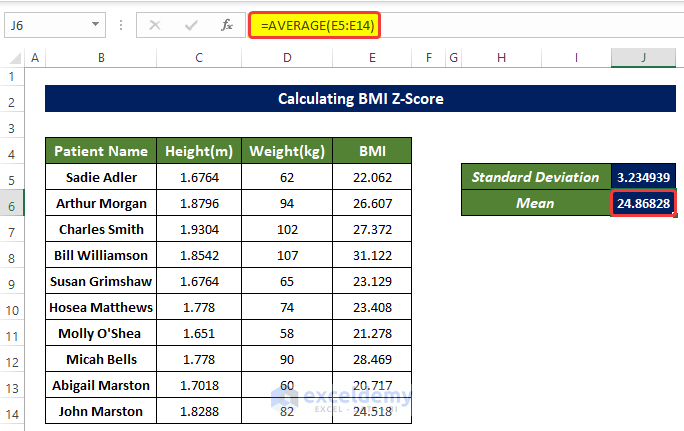
- Select J6 and use the formula:
=AVERAGE(E5:E14)- It will calculate the mean of data in E5:E14.
Step 4 – Calculate the Z Score
Steps
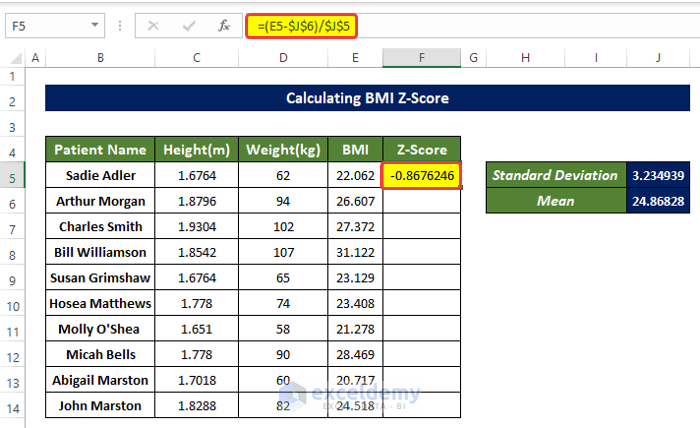
- Select F5 and enter the following formula:
=(E5-$J$6)/$J$5
- It will calculate the Z-Score of the BMI value in E5.
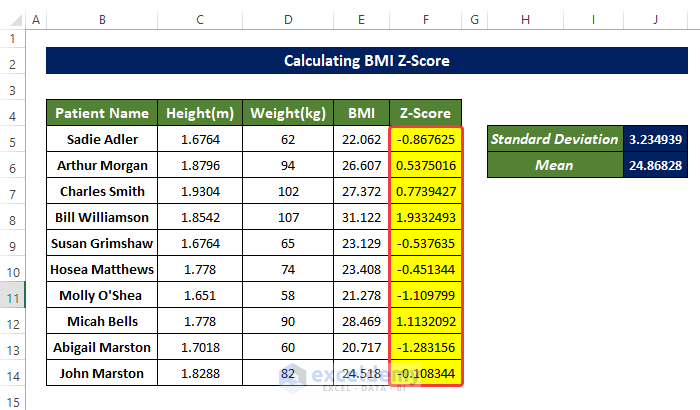
- Drag down the Fill Handle to see the result in the rest of the cells.
An Alternative Way to Calculate the Z Score
Steps
- Select F5 and enter the following formula
=STANDARDIZE(E5,$J$6,$J$5)
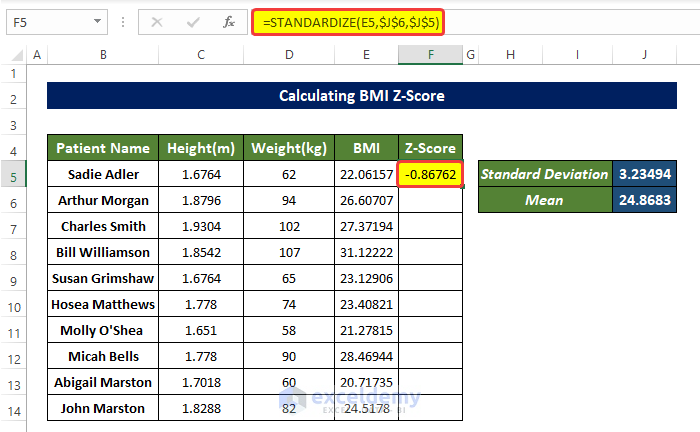
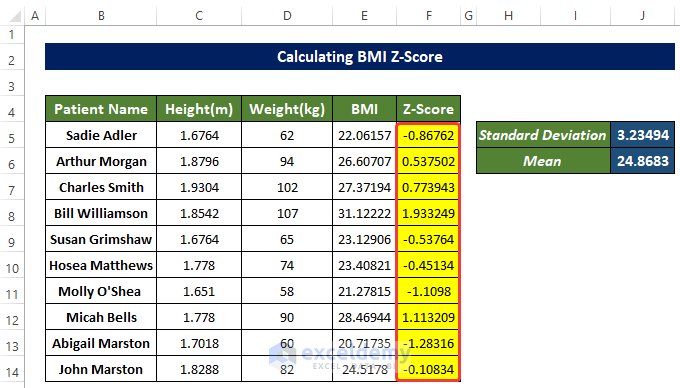
- Drag down the Fill Handle to see the result in the rest of the cells.
Download Practice Workbook
Download the practice workbook.
<< Go Back to BMI | Formula List | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!

