The basic formula for cosine squared, also known as the Pythagoras trigonometric formula, can be presented in the following format:
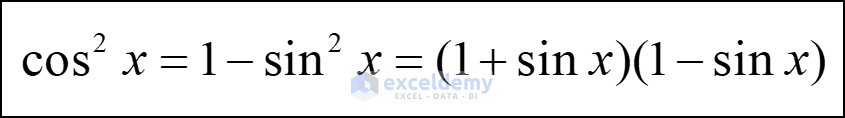
- Another expression of cosine squared, lseer known but still used in differential calculus is as follows:

- We can convert and create various other entities from this cosine squared value, for example the sine squared value. Using both sine and cosine squared values, we can also extract the tangent squared values, which leads to all the other components of trigonometry.
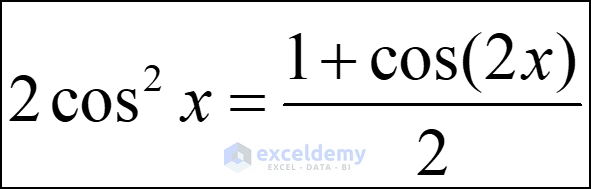
Read More: Why Cos 90 Is Not Equal to Zero in Excel?
How Can We Write Cos Squared in Excel?
In order to write Cos squared values in Excel, we use the COS function .
Steps
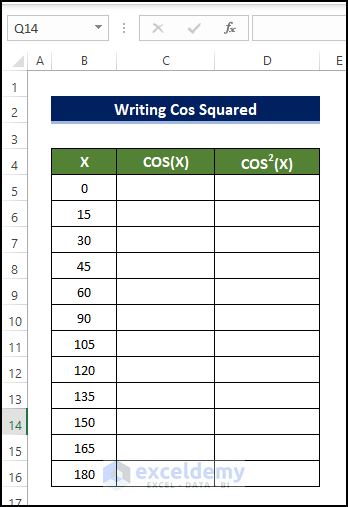
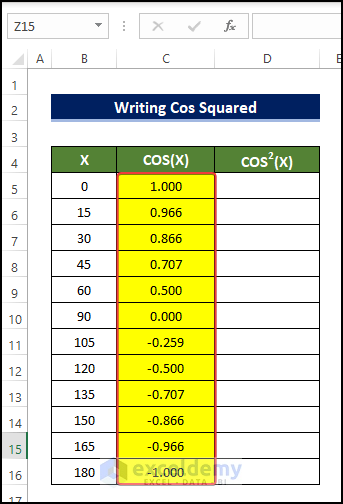
- Our dataset contains a set of angles in the range B5:B16.
- We will derive the cosine and cosine squared values of these angles.
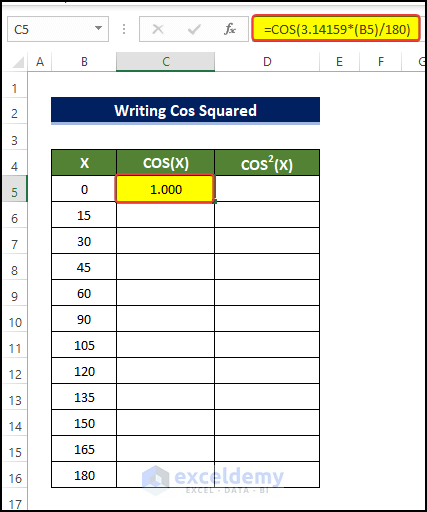
- Select cell C5 and enter the formula:
=COS(3.14159*(B5)/180)
Note
Since the angle argument in the COS function must be in radian units, not degrees, our formula converts the degree value of the angle into the radian unit.
- Drag the Fill Handle to cell C16.
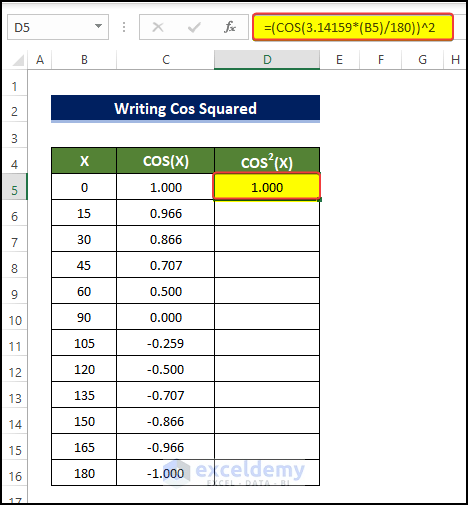
- To round up the values, select cell D5 and enter the following formula:
=(COS(3.14159*(B5)/180))^2
- Drag the Fill Handle to cell D16.
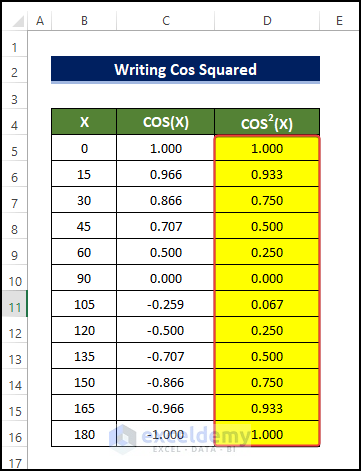
Use of Cos Squared in Excel
Method 1 – Cos Squared in Excel for Angles in Radians
Steps
- Our dataset includes angles in radian units in the range B5:B9
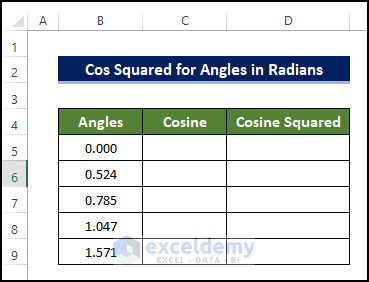
- Select cell C5 and enter the following formula:
=COS(B5)
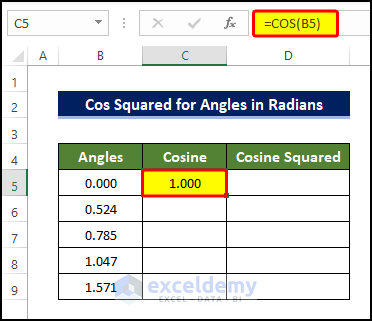
- Press ENTER to execute the formula
- Drag the Fill Handle icon to the bottom of the Cosine column to copy the formula.
The result is as follows:
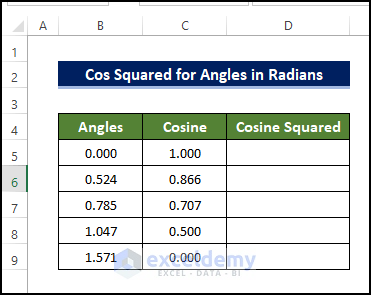
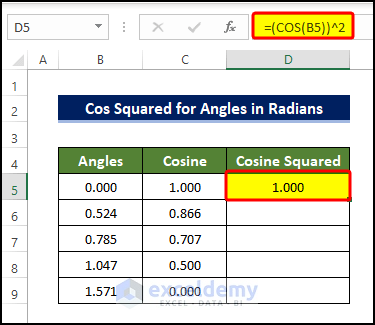
- To calculate the cos squared value, select cell D5 and enter the following formula:
=(COS(B5))^2
- Press ENTER to execute the formula.
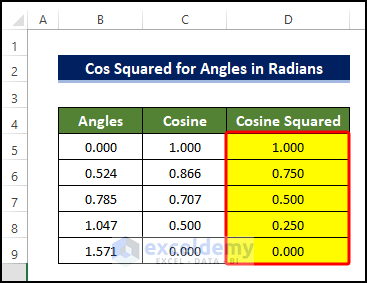
- Drag the Fill Handle to the end of the Cosine column to copy the formula.
The result is as follows:
Method 2 – Cos Squared in Excel for Angles in Degrees
This method requires converting the angle values from degrees to radians, as the COS function accepts only angles in radians.
Steps
- Select cell C5 and enter the formula:
=COS(B5*PI()/180)
- Press ENTER to execute the formula.
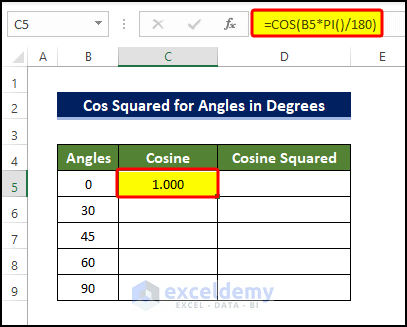
- Drag the Fill Handle icon to the end of the Cosine column to copy the formula.
The result is as follows:
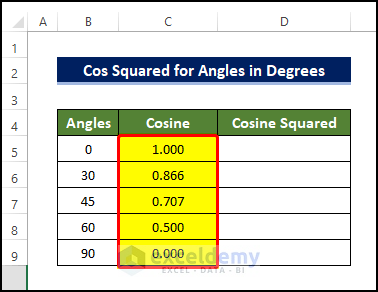
- To calculate the cos squared value, select cell D5 and enter the following formula:
=(COS(B5*PI()/180))^2
- Press ENTER to execute the formula.
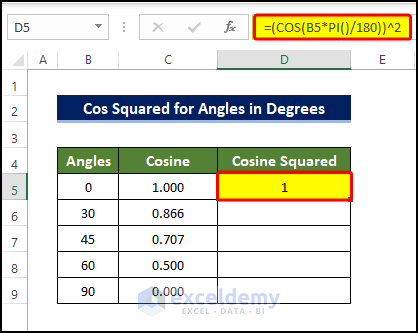
Note
Degree values must be converted into radian units for use with the COS function.
- Drag the Fill Handle icon to the end of the Cosine column to copy the formula.
The result is as follows:
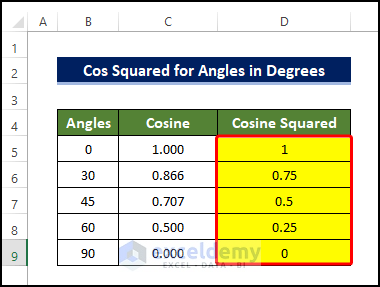
Method 3 – Embedding VBA Code to Find Cos Squared of an Angle
Steps
- Click the Developer tab and select Visual Basic. If you don’t see the Developer tab, you will have to enable the Developer tab. Alternatively, you can press Alt+F11 to open the Visual Basic Editor.
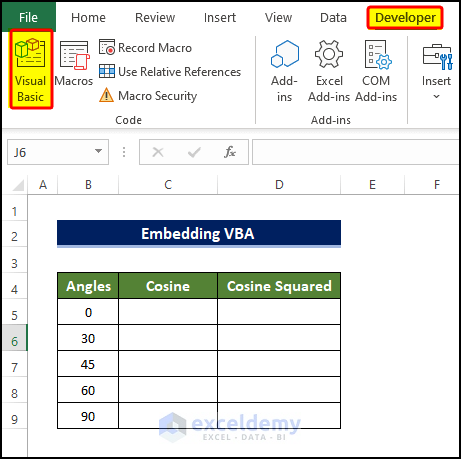
- A new dialog box will open. In it, click on Insert > Module.
- A Module editor window opens. In it, enter the following code
Sub Cosine_squared()
Dim rng As Range, c As Range
On Error Resume Next
Set rng = Application.InputBox( _
Title:="Exceldemy", _
Prompt:="Select the range of cell that are goin to be Cosine Squared", _
Type:=8)
On Error GoTo 0
For Each c In rng
c.Offset(0, 1).Value = Cos(c.Value * 3.1416 / 180)
c.Offset(0, 2).Value = (Cos(c.Value * 3.1416 / 180)) ^ 2
c.Offset(0, 1).Select
Selection.Value = Format(ActiveCell, "#.00")
c.Offset(0, 2).Select
Selection.Value = Format(ActiveCell, "#.00")
Next
End Sub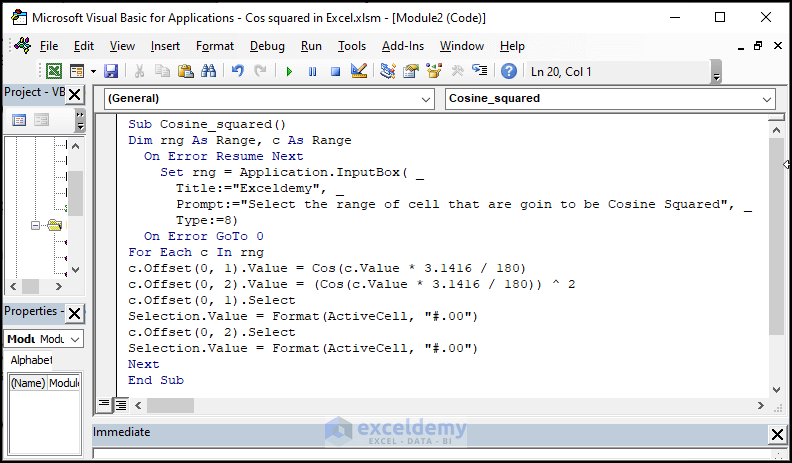
- Close the Module window.
- Select the View tab, then Macros.
- Click on View Macros.
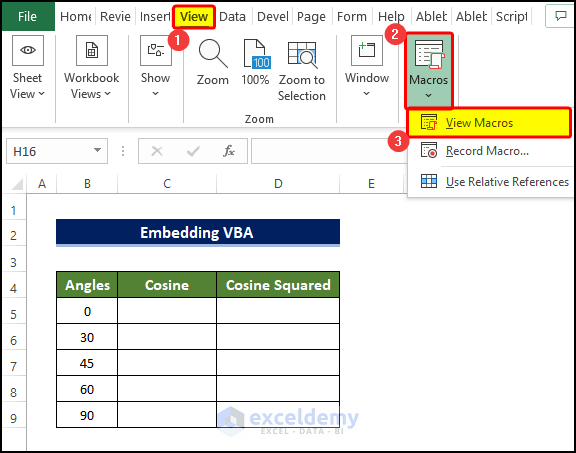
- Select the macro that you just created, named Cosine_squared.
- Click Run.
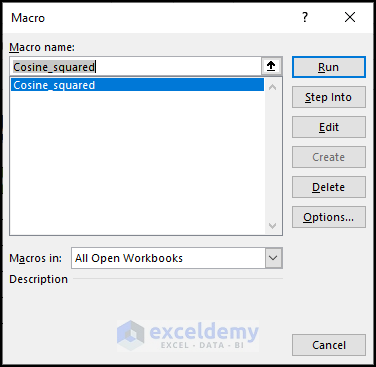
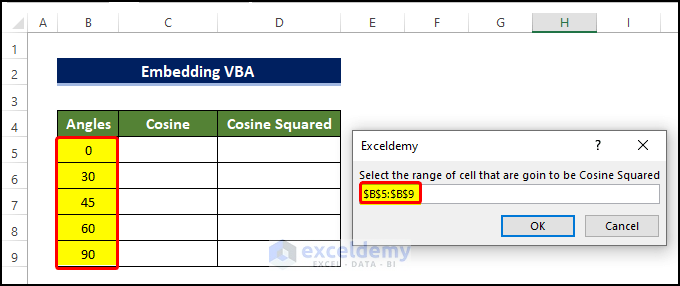
- A range box opens, requesting the range to be Cosine squared.
- Select the range B5:B9.
- Click OK.
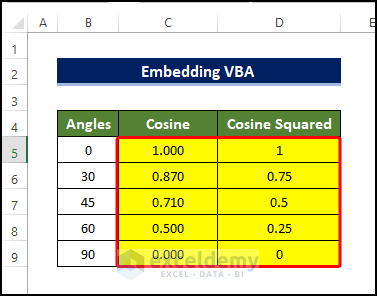
- The range C5:C9 is filled with the cosine value of the angles in the range B5:B9.
- The range D5:D9 is filled with the cosine squared value of the angles in the range B5:B9.
What Is the Difference Between Cos^2 (x) and Cos (x)^2?
The short answer is that Cos2x = (Cos x)2. Conversely, Cos(x)2 is equal to the Cosine of the squared value of x, a totally different value.
To demonstrate, if the angle value (x) is equal to 30, the value of Cos2x will be:

And the value of Cos(x)2 will be:

Hope this clears up your confusion about this topic.
Things to Remember
- The COS function in Excel expects the radian unit of angle, not the degree value, so degree values will need to be converted into radian units by multiplying the angle by (pi/180).
- Pay attention to the power over trigonometry functions, ie whether the power is over the angle or over the cosine itself, because these values represent different things.
Download Practice Workbook
Related Article
<< Go Back to Excel COS Function | Excel Functions | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!

