How to Find Z Critical Value in Excel?

We carry out various operations in Excel. We can also perform many different mathematical and statistical tasks in the Excel workbook. In some cases, you may need to calculate the Z Critical Value. This value plays a significant role in the Hypothesis Tests. In a hypothesis test, the Test Statistic is the result. But, you have to find out if this result is statistically significant or not. To determine that, you ought to make comparisons between the test statistic and the Z critical value. Therefore, in this article, we’ll show you the suitable examples to Find Z Critical Value in Excel.

Introduction to NORM.S.INV Function

The NORM.S.INV function in Excel determines the inverse of the standard normal cumulative distribution. The Mean is Zero and the Standard Deviation is One in the cumulative distribution.

• Syntax

=NORM.S.INV(probability)

• Arguments

probability: A probability corresponding to the standard normal cumulative distribution is required.

How to Find Z Critical Value in Excel: 3 Suitable Examples

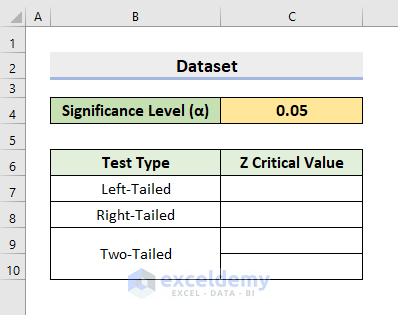
To know if our hypothesis test results are statistically significant, we have to compare the test statistic and the Z critical value. The absolute value of the test statistic needs to be greater than the Z critical value to be considered statistically significant. To illustrate, we’ll use a sample dataset as an example. For instance, in the following dataset, we have a Significance Level (α) that is 0.05. Here, we’ll compute the Z critical value for 3 different test types. So, go through the below examples to find Z Critical Value in Excel.

1. Calculate the Z Critical Value in the Left-Tailed Test

In our first example, we’ll calculate the Z critical value for the Left-Tailed test. You’ll find the critical value as output for this test. Here, we’ll apply the Significance Level (α) as a probability in the argument of the NORM.S.INV function. Thus, follow the steps below to perform the task.

STEPS:

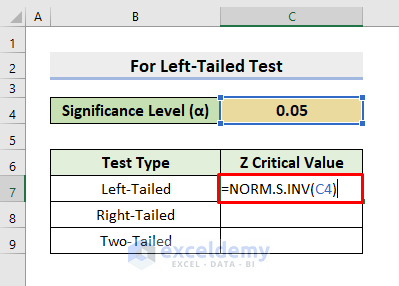
• First, select cell C7.
• Then, type the following formula:

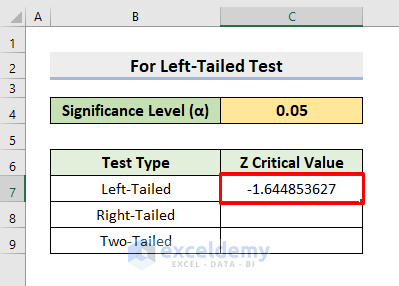
• After that, press Enter to return the value.
• As a result, you’ll get the desired result.
• See the picture below to have a better understanding.

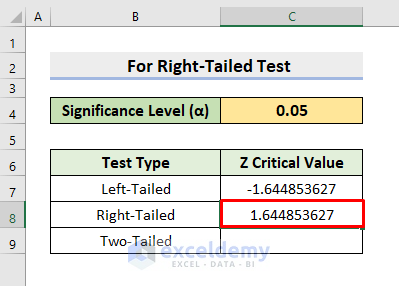
2. Find Z Critical Value in Excel for Right-Tailed Test

The Right-Tailed test is our second case. Like the left-tailed, there is also one critical value as output. In this example, we’ll modify the Significance Level (α) to insert it in the argument of the NORM.S.INV function. In the right-tailed test case, we need to subtract the Significance Level from 1. Hence, learn the following steps to carry out the operation.

STEPS:

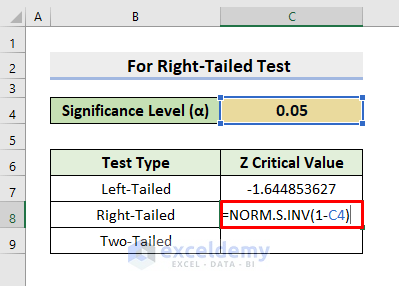
• Firstly, choose the C8
• Next, insert the below formula:

• Subsequently, get the result by pressing Enter.
• Thus, it’ll return the Z critical value for the right-tailed test.

Read More: How to Find T Critical Value in Excel

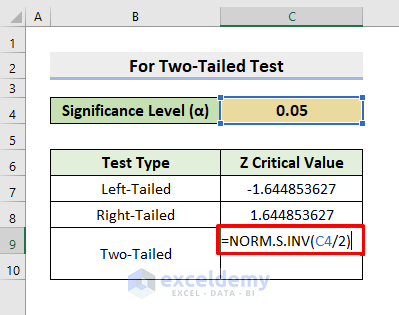
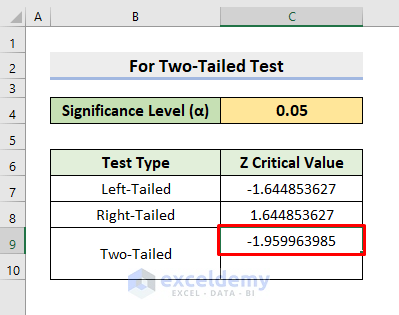
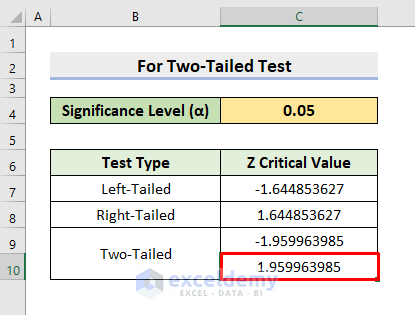
3. Get Z Critical Value for Two-Tailed Test in Excel

In our last example, we’ll show the process to get the Z Critical Value for the Two-Tailed test in Excel. Here, you’ll get 2 critical values as output. We’ll input the Significance Level (α) as a probability in the argument of the NORM.S.INV function. But, we have to edit it first. As it’s two-tailed, we’ll divide the Significance Level by 2 to get one critical value. Then, to get another critical value, we’ll subtract the division output from 1. Therefore, see the steps below to determine the values.

STEPS:

• Click the cell C9 at first.
• Afterward, type the formula:

• Lastly, press Enter and it’ll return the result.

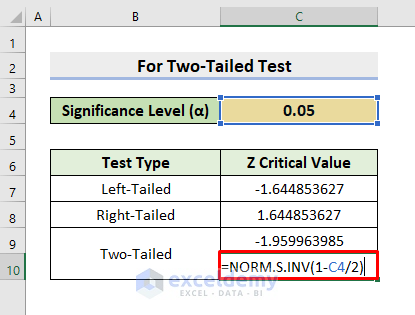
• Again, to get another critical value, choose cell C10.
• Then, input the formula:

• Consequently, press Enter.
• At last, you’ll get the precise Z critical value.
• In this way, the two critical values for the two-tailed test will appear.

Download Practice Workbook

Download the following workbook to practice by yourself.

Conclusion

Henceforth, you will be able to Find Z Critical Value in Excel following the above-described examples. Keep using them and let us know if you have more ways to do the task. Don’t forget to drop comments, suggestions, or queries if you have any in the comment section below.

Related Articles

• How to Find F Critical Value in Excel
• How to Find Critical Value of r in Excel
• How to Find Chi-Square Critical Value in Excel

<< Go Back to Critical Value in Excel | Excel for Statistics | Learn Excel