If you are looking for zero coupon bond price calculator in Excel, this article is for you. Here, we will demonstrate to you 5 simple, easy, and effective examples to do the task smoothly.
What Is Zero Coupon Bond?
When a bond does not pay coupon payments or interest and trades but rather pays a bulk amount of money at the time of maturity, it is called a Zero Coupon bond. A Zero Coupon bond is also known as a “deep discount bond” or “discount bond”. The sum of money paid at maturity is called the face value. Since a Zero Coupon bond provides no coupons or interest and trades, its transaction occurs at a discount to its face value.
Zero Coupon Bond Price Calculator Excel: 5 Examples
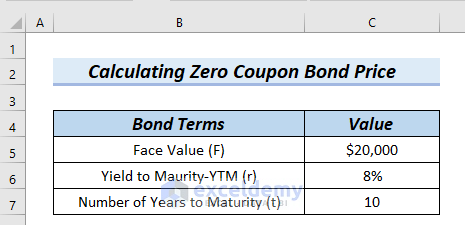
The following table has Bond Terms and Value columns. We will use this table for the zero coupon bond price calculator in Excel. For this, we will go through 5 easy and effective examples. Here, we used Excel 365. You can use any available Excel version.
1. Applying Generic Formula to Create Zero Coupon Bond Price Calculator in Excel
In this method, we will use the generic formula for Zero Coupon Bond Price Calculator in Excel.
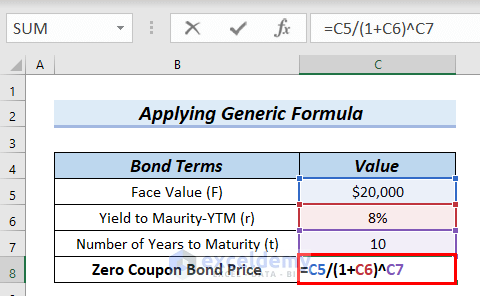
We know, the generic formula for Zero Coupon Price Calculation = (Face Value)/〖(1+r)〗^t
Steps:
- First, we will type the following formula in cell C8.
=C5/(1+C6)^C7Formula Breakdown
- (1+C6) → adds 1 with cell C6.
- (1+8%) → Therefore, this becomes
- Output: 1.08
- (1+C6)^C7 → is (1.08)^10
- (1.08)^10 → As a result, it becomes
- Output: 2.158924997279
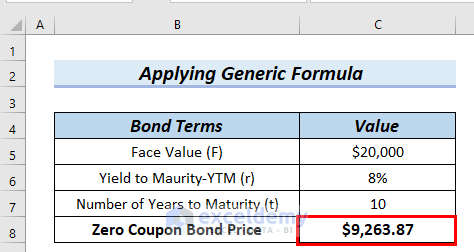
- C5/(1+C6)^C7 → divides 20000 by 2.158924997279
- 20000/2.158924997279→ Hence, it becomes
- Output: $9263.87
- Explanation: Finally, $9263.87 is the Zero Coupon Bond Price.
- After that, press ENTER.
As a result, you can see the calculated Zero Coupon Bond Price in cell C8.
Read More: How to Create Convertible Bond Pricing Model in Excel
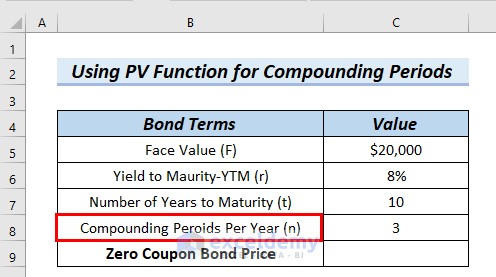
2. Zero Coupon Bond Price Calculator for Compounding Periods
In this method, we will describe the generic formula including compounding periods per year for Zero Coupon Bond Price Calculator in Excel.
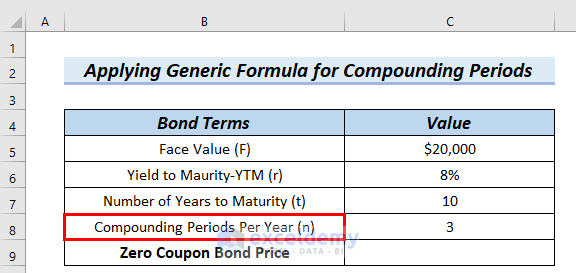
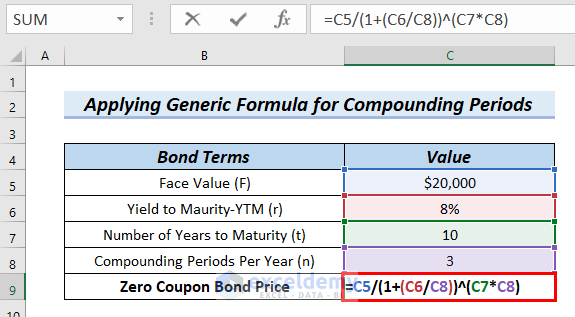
We know, the generic formula including compounding periods per year= (Face Value)/〖(1+r/n)〗^t*n
In the following table, we can see the Value for Compounding Periods Per Year (n) is 3. We will use the above formula for Zero Coupon Price Calculation.
Steps:
- First of all, we will type the following formula in cell C9.
=C5/(1+(C6/C8))^(C7*C8)Formula Breakdown
- (C7*C8) → It multiplies cell C7 with cell C8
- (10*3) → Therefore, it becomes
- Output: 30
- (C6/C8) → divides cell C6 by cell C8
- (8%/3) → Then, it becomes
- Output: 0.026666666667
- (1+(C6/C8)) → is adding 1 with 0.026666666667
- (1+0.026666666667) → As a result, this becomes
- Output: 1.026666666667
- (1+(C6/C8))^(C7*C8) → is (1.026666666667)^30
- (1.026666666667)^30 → Then, it becomes
- Output: 2.2033739695385
- C5/(1+(C6/C8))^(C7*C8) → is dividing C5 by 2.2033739695385.
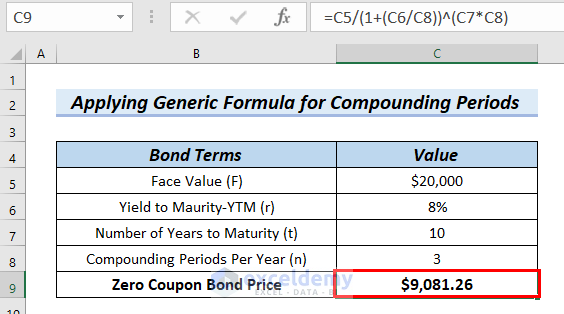
- 20000/2.2033739695385 → becomes
- Output: $9081.26
- Explanation: Finally, $9081.26 is the Zero Coupon Bond Price.
- At this point, press ENTER.
Therefore, you can see the calculated Zero Coupon Bond Price in cell C9.
Read More: How to Make Treasury Bond Calculator in Excel
3. Using PV Function to Create Zero Coupon Bond Price Calculator in Excel
Here, we will use the PV function for Zero Coupon Bond Price Calculator in Excel.
Steps:
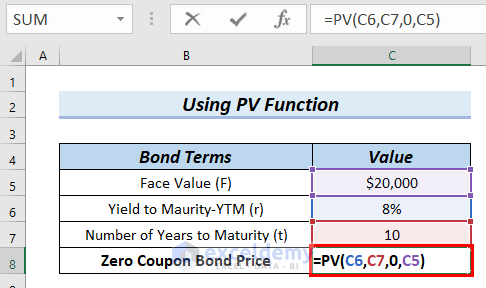
- In the beginning, we will type the following formula in cell C8.
=PV(C6,C7,0,C5)Formula Breakdown
- PV(C6,C7,0,C5) → The PV function calculates the present value of a loan or investment based on a constant interest rate.
- C6 is the rate, which is referred to as Yield to Maturity (YTM)
- C7 is the nper, which is the total number of payment periods
- 0 is the pmt, that is the payment made on each period. For zero coupon bond, as there is no periodic payment, pmt is 0
- C5 is the fv, which is the Future Value
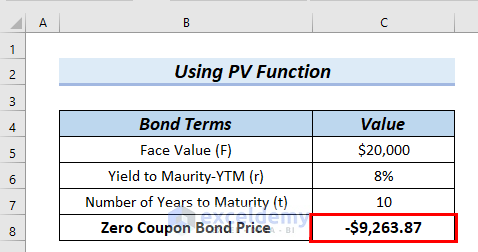
- PV(8%,10,0,20000) → Therefore, this becomes
- Output: -$9263.87, here the negative sign means outgoing cash flow.
- Explanation: As a result, -$9263.87 is the Zero Coupon Bond Price.
- Next, press ENTER.
Finally, you can see the calculated Zero Coupon Bond Price in cell C9.
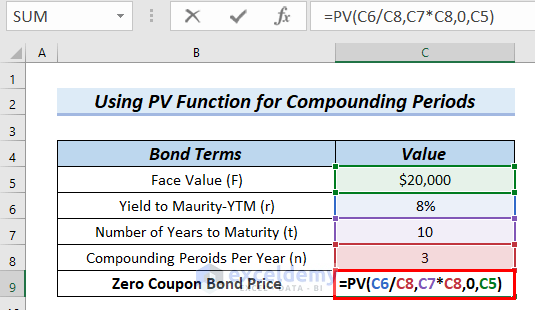
4. Use of PV Function to Make Zero Coupon Bond Price Calculator for Compounding Period
In this method, we will show how to use the PV function when compounding periods per year are included for Zero Coupon Bond Price Calculator in Excel.
In the following table, we can see the Value of Compounding Periods Per Year (n) is 3. Now, we will describe steps for calculating zero coupon bond price.
Steps:
- Firstly, we will type the following formula in cell C9.
=PV(C6/C8,C7*C8,0,C5)Formula Breakdown
- PV(C6/C8,C7*C8,0,C5) → The PV function calculates the present value of a loan or investment based on a constant interest rate.
- C6/C8 is the rate, which is referred to as Yield to Maturity (YTM)
- 8%/3 → Therefore, it becomes
- Output: 0.026666666667
- C7*C8 is the nper, which is the total number of payment periods
- 10*3 → As a result, becomes
- Output: 30
- 0 is the pmt, that is the payment made on each period. For zero coupon bond, as there is no periodic payment, pmt is 0
- C5 is the fv, which is the Future Value
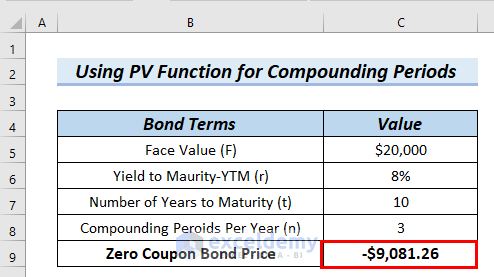
- PV(0.026666666667,30,0,20000) → becomes
- Output: -$9081.26, here the negative sign means outgoing cash flow.
- Explanation: As a result, -$9081.26 is the Zero Coupon Bond Price
- Next, press ENTER.
Finally, you can see the calculated Zero Coupon Bond Price in cell C9.
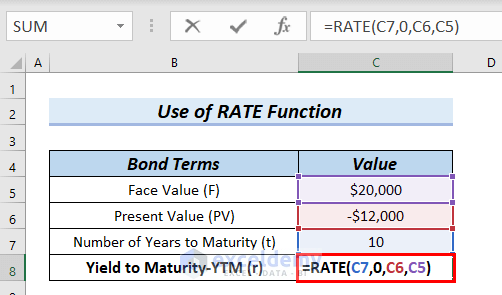
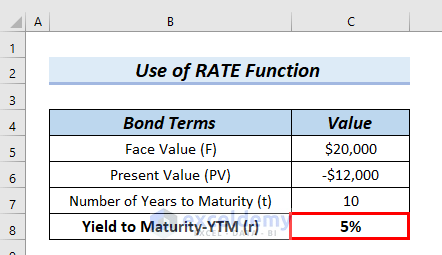
5. Using RATE Function to Calculate Interest Rate for Zero Coupon Bond
In this method, we will use the RATE function to calculate the Yield to Maturity-YTM (r), which is the interest rate (r) for a zero coupon bond.
Steps:
- First, we type the following function in cell C8.
=RATE(C7,0,C6,C5)Formula Breakdown
- RATE(C7,0,C6,C5) → the RATE function returns the interest rate per period of an annuity.
- C7 is the npr, which is the total number of payment periods
- 0 is the pmt, that is the payment made on each period. For zero coupon bond, as there is no periodic payment, pmt is 0
- C6 is pv, which is the Present Value
- C5 is fv, that is the Future Value
- RATE(10,0,-12000,20000) → Therefore, it becomes
- Output: 5%
- Explanation: Finally, 5% is the Yield to Maturity-YTM (r) for zero coupon bond price
- Afterward, press ENTER.
As a result, we can see the Yield to Maturity-YTM (r) for zero coupon bond price in cell C8.
Practice Section
You can download the above Excel file to practice the explained methods.
Download Practice Workbook
Conclusion
Here, we tried to show you 5 examples of zero coupon bond price calculator in Excel. Thank you for reading this article, we hope this was helpful. If you have any queries or suggestions, please let us know in the comment section below.
<< Go Back to Bond Price Calculator | Finance Template | Excel Templates
Get FREE Advanced Excel Exercises with Solutions!