This tutorial will demonstrate how to use Excel Solver to determine which projects should be undertaken. Companies need to know which projects should undertake in order to produce the greatest NPV (net present value) when there are very few resources. Applying Excel Solver can help solve this kind of problem. We often apply it directly to predict the outcome or help in decision-making. So, it is important to learn how to use Excel solver to determine which projects should be undertaken.
What Is an Excel Solver?
Excel Solver is used in many different algorithms for finding the solution to different complex linear and non-linear problems. The methods of Excel Solver are.
GRG Nonlinear: The full form of this method is the Generalized Reduced Gradient Nonlinear method. We will use this method when simple nonlinear problems where the data will contain a minimum of one constraint.
LP Simplex: We will use Excel Solver for Linear Programming problems when linear relationships occur. With the linear connection with the data, linear programming tends to achieve the desired goal such as minimum loss, maximum profit, etc.
Evolutionary: Among all the types, this is the most difficult where you can not determine the characteristics of the function. The system of this kind of function can increase or decrease at any time. This is because the functions are either discontinuous or nonsmooth.
How to Enable Excel Solver
Normally, Excel Solver isn’t available in the Data tab. We have to add it manually to our menu tab. We can add and enable Excel by following the below process:
- First, go to the File option.
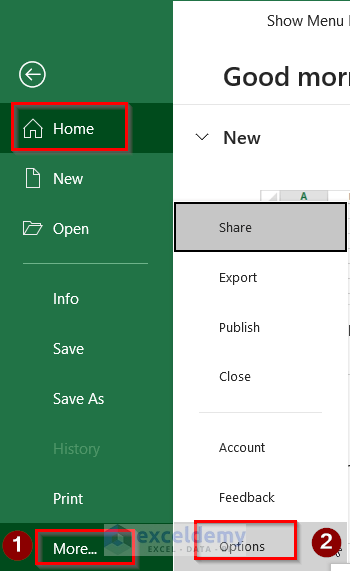
- Then, go to More… > Options.
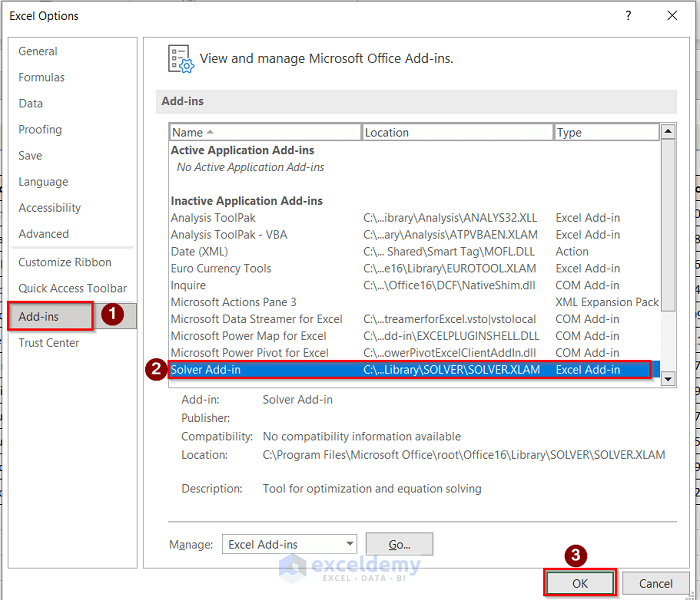
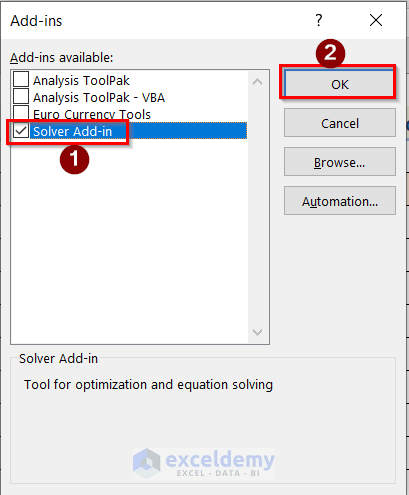
- Next, go to Add-ins > Solver Add-ins > OK options.
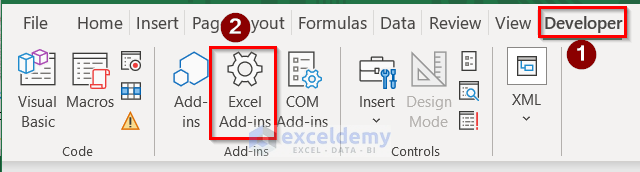
- After that, in the Developer tab select the Excel Add-ins option.
- Afterward, tick the Solver Add-in option and press OK.
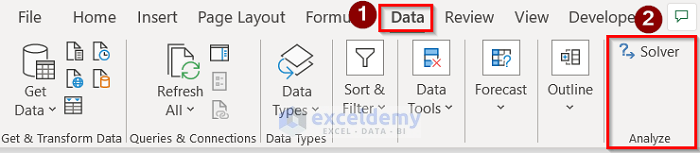
- Finally, go to Data > Solver options to open the Solver Parameters dialog box.
How to Use Excel Solver to Determine Which Projects Should Be Undertaken: 3 Cases
We’ll use a sample dataset overview as an example in Excel to understand easily. If you follow the steps correctly, you should learn how to use Excel Solver to determine which projects should be undertaken on your own. The steps are:
1. Maximizing NPV to Determine Which Projects Should Be Undertaken
In this case, our goal is to use an Excel solver to determine which projects should be undertaken by maximizing NPV in Excel. In this case, the project that has maximum NPV will always undertake the project. The steps of this process are.
Steps:
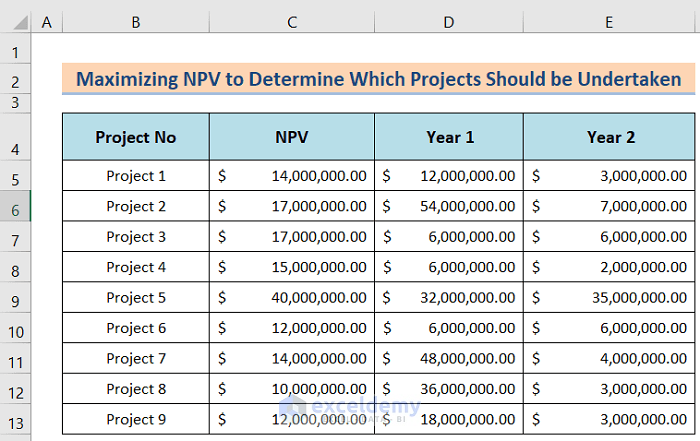
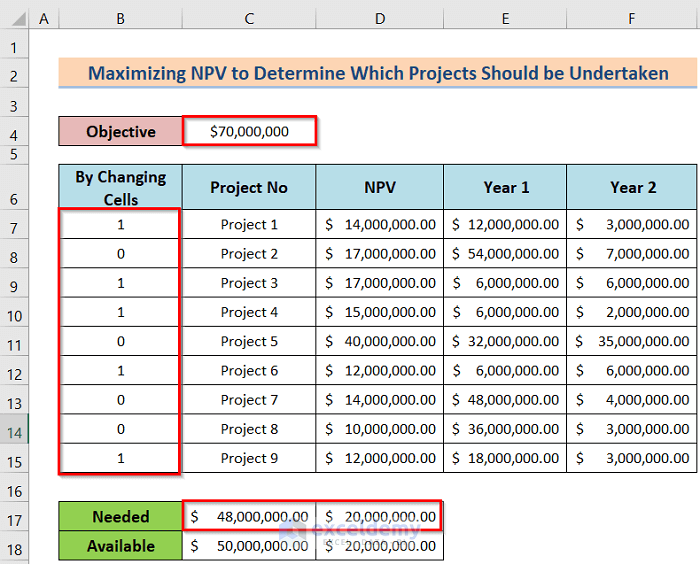
- First, arrange a dataset like the below image. In this case, we have Project No in cell B4, NPV in cell C4, Year 1 in cell D4, and Year 2 in cell E4.
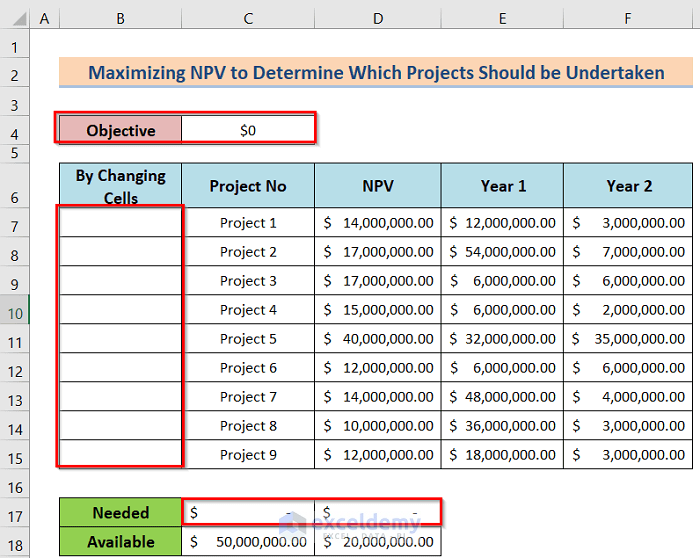
- Next, add more cells like Objective, By Changing Cells, and Needed We will use these three parameters to use the solver option correctly.
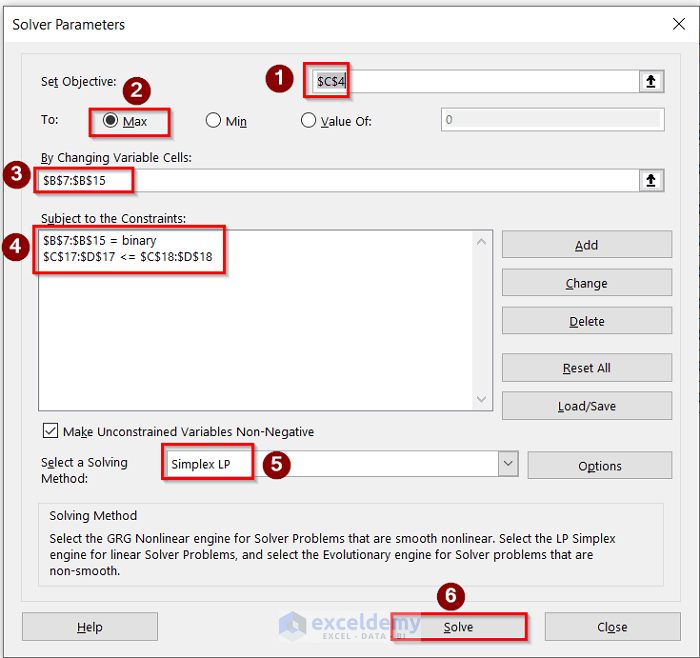
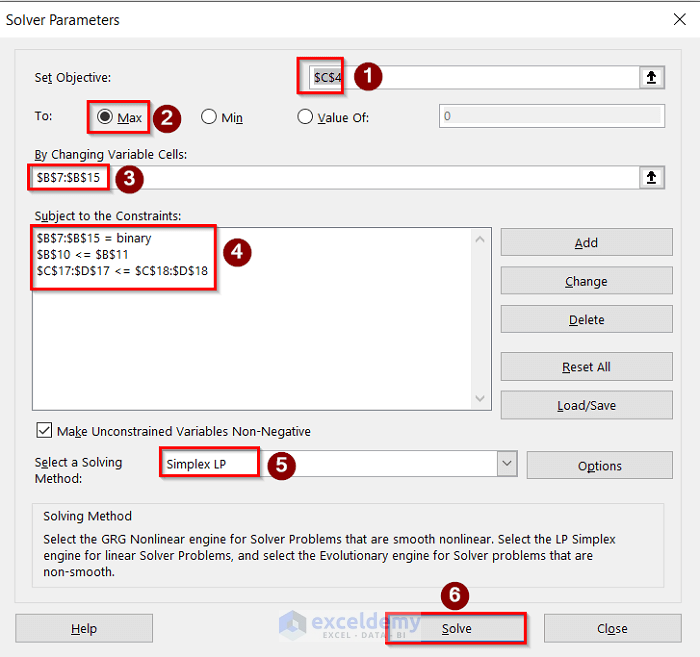
- After that, go to Data>Solver options to open the Solver Parameters dialog box. In the Solver Parameters dialog box, fulfill the Set Objective, To, By Changing Variable Cells, Subject to Constraints, and Select a Solving Method After that, press the Solve option to get the desired result.
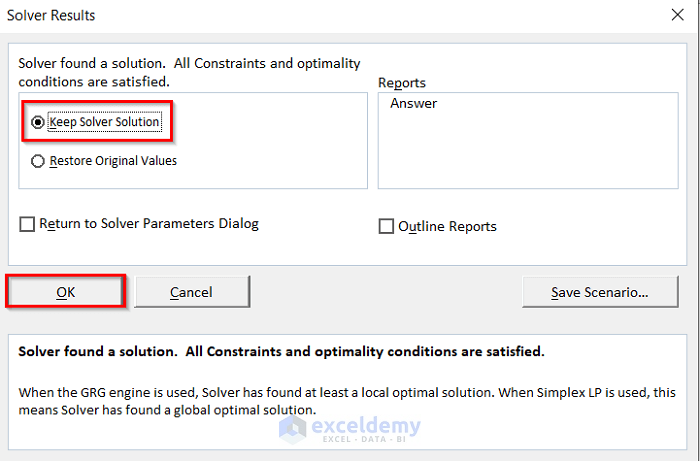
- Afterward, you will get the Solver Results dialog box. Here, select the Keep Solver Solution and press OK.
- Finally, you will get the desired result like the following image.
Read More: How to Do Portfolio Optimization Using Excel Solver
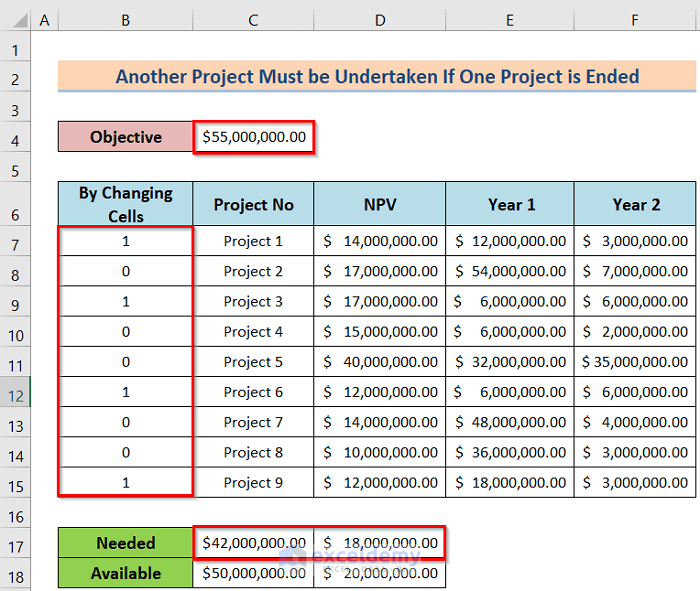
2. Another Project Must be Undertaken If One Project is Ended
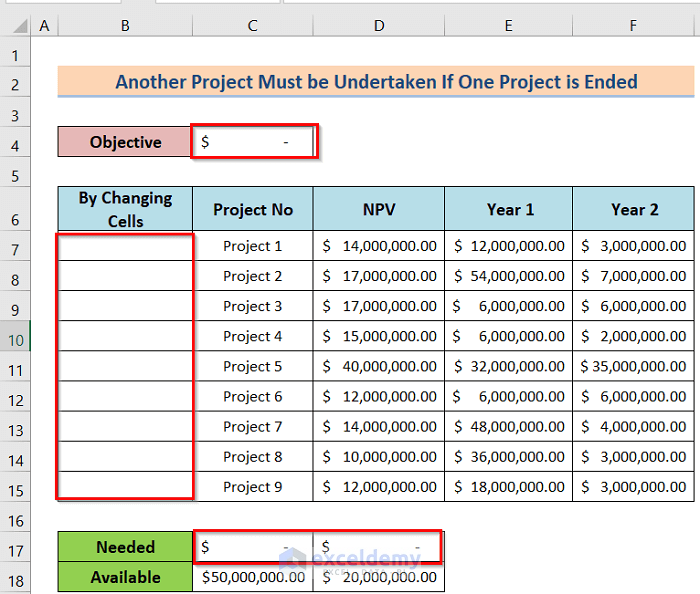
Suppose that if project 4 is undertaken, project 5 must be undertaken. The model, in this case, will be the same as that in case 1 except for a new constraint. Therefore, the worksheet will look the same as that in case 1. We will describe the full process in the below steps.
Steps:
- First, arrange a dataset like the below image.
- Second, go to Data > Solver options to open the Solver Parameters dialog box. In the Solver Parameters dialog box, fulfill the Set Objective, To, By Changing Variable Cells, Subject to Constraints, and Select a Solving Method After that, press the Solve option to get the desired result.
- Last, you will get the desired result like the following image.
Read More: How to Use Excel Solver for Linear Programming
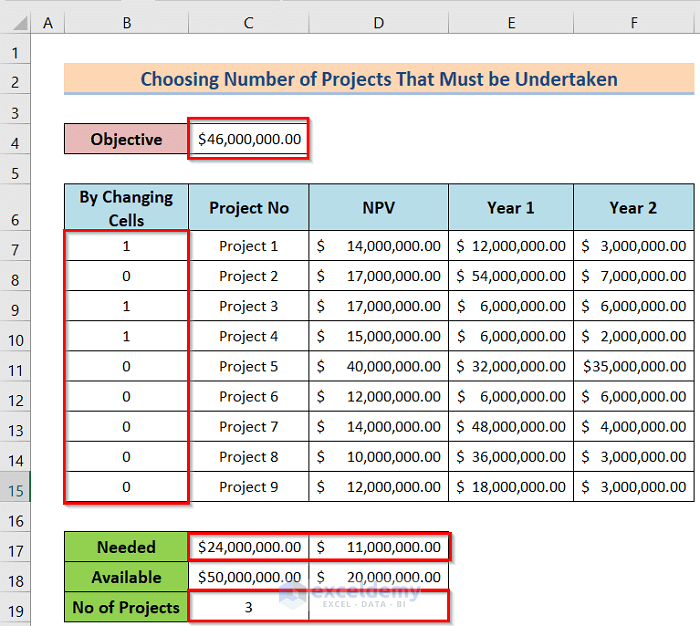
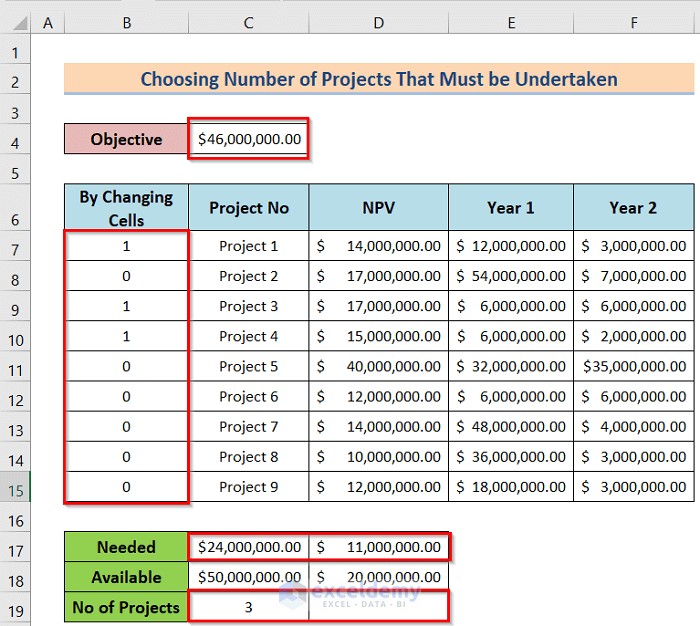
3. Choosing the Number of Projects That Must be Undertaken
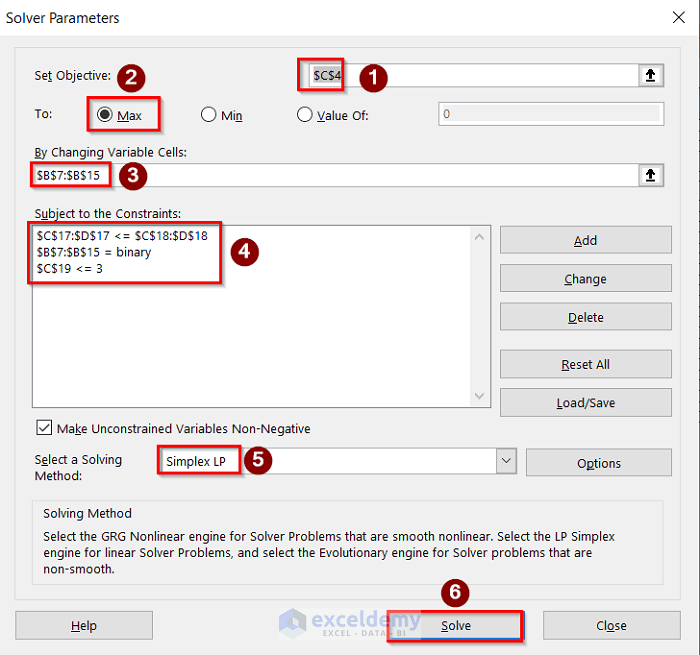
Now, suppose that you can do only three projects among those 9 projects. The model, in this case, will be the same as that in case 2 except for a new constraint. Therefore, the worksheet will look the same as that in case 2. We will describe the full process in the below steps.
Steps:
- To begin with, arrange a dataset like the below image.
- In addition, go to Data > Solver options to open the Solver Parameters dialog box. In the Solver Parameters dialog box, fulfill the Set Objective, To, By Changing Variable Cells, Subject to Constraints, and Select a Solving Method After that, press the Solve option to get the desired result.
- Finally, you will get the desired result like the following image.
Read More: Example with Excel Solver to Minimize Cost
Things to Remember
- Excel Solver isn’t normally added in the Data tab. So, at the very beginning, add it to your Data tab by following the above description.
- The most important thing is to focus while using the Solver Parameters dialog box. Any mistake in the dialog box will cause a different result in this case.
- All the main formulas must be checked properly before using the Solver If you have any problems with formulas or data then you have to correct them before using the Solver option.
Download Practice Workbook
You can download the practice workbook from here.
Conclusion
Henceforth, follow the above-described methods. Hopefully, these methods will help you learn to use Excel solver to determine which projects should be undertaken. We will be glad to know if you can execute the task in any other way. Please feel free to add comments, suggestions, or questions in the section below if you have any confusion or face any problems. We will try our best to solve the problem or work with your suggestions.
Related Articles
- How to Use Excel Solver to Rate Sports Team
- Solving Sequencing Problems Using Excel Solver Solution
- Solving Transportation or Distribution Problems Using Excel Solver
- How to Assign Work Using Evolutionary Solver in Excel
- Resource Allocation in Excel
- How to Create Financial Planning Calculator in Excel
- Solving Equations in Excel
<< Go Back to Excel Solver Examples | Solver in Excel | Learn Excel
Get FREE Advanced Excel Exercises with Solutions!